|
PETIT
EXEMPLE
|
Une Méthode pour la détection et l'analyse des réseaux de collaborations dans le domaine de la recherche scientifique.
|
PETIT
EXEMPLE
|
Une Méthode pour la détection et l'analyse des réseaux de collaborations dans le domaine de la recherche scientifique.
L'exemple que je vous propose ici a fait l'objet d'une publication au VSST'95 dont voici le titre l'auteur et le resumé:
L'objet de cet article qui s'inscrit dans le cadre de la Veille Technologique et Scientifique est de proposer une méthode de détection et de suivi des équipes de recherche à travers les collaborations qui existent entre chercheurs. L'information utilisée pour reconstituer les réseaux de collaborations est issue de banques de données structurées de type bibliographique. Ces réseaux formels permettent de découvrir les alliances cachées, de détecter les équipes isolées, de saisir les transferts de technologies, etc.. Cet article abordera notamment la méthode de passage des données bibliographiques à l'élaboration des réseaux de cosignature et les méthodes d'analyse de données qui permettent de mettre en évidence les différences de densité dans ces réseaux. Ces méthodes seront illustrées par un exemple.
Après extraction des données nous avons récolté plus de 5600 auteurs. Une première simplification du problème a consisté à éliminer tout les auteurs qui n'ont publié qu'une seule fois. Ceci a ramené le nombre d'auteurs aux environs de 1400. Du point de vue recherche de réseaux de collaboration cette première simplification de prête pas à conséquence puisqu' un auteur qui n'a publié qu'une seule fois ne pourra jamais être l'intermédiaire entre deux auteurs qui ne sont pas déjà en relation.
Une deuxième simplification a consisté à ne croiser tout les auteurs restants qu'avec les auteurs les plus prolifiques en l'occurrence 94 auteurs qui ont publié plus de six fois. Nous avons aussi éliminé tous les auteurs qui n'ont jamais publié avec les 94 "grands" chercheurs ce qui nous a ramenés à 524 auteurs. Le résultat du croisement est une matrice T de taille 524x94.
L'application
de nos algorithmes de recherche de réseaux indépendants de collaborations
nous donne le résultat suivant:

L'existence des réseaux est traduite par la structure diagonale par bloc
de la matrice.
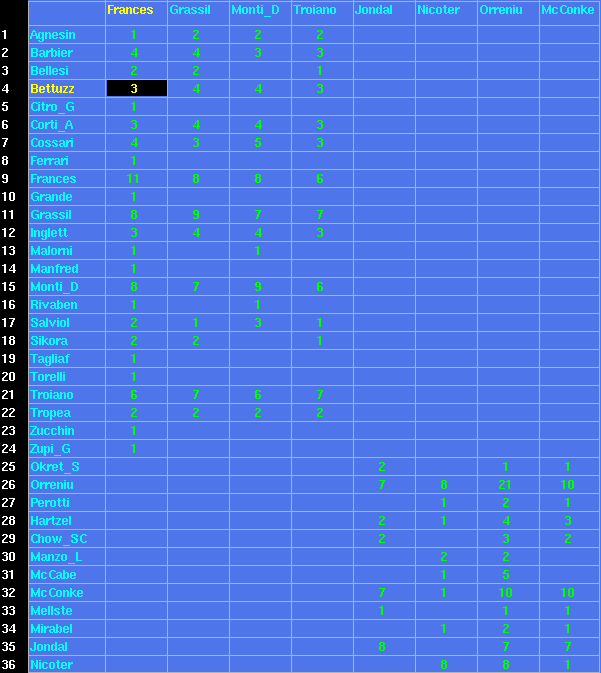
Intéressons nous maintenant au réseau qui contient Oreniu un des premiers chercheurs à s'intéresser à l'apoptose. Ce réseau correspond au deuxième bloc et contient 37 auteurs dont 8 "grands". La matrice associé à ce réseaux est la suivante:
Nous remarquons que telle qu'elle se présente cette matrice ne trahit
aucune forme particulière que pourrait avoir ce réseau.
Nous appliquons une AFC sur cette matrice de contingence et nous obtenons la carte factorielle suivante:
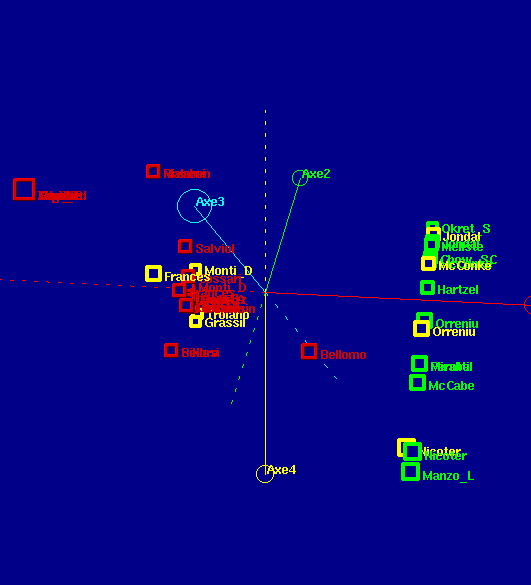
Bellesi, Sikora, Agnesin, Rivaben,Malorni} groupe 4={Tagliaf,Citro,Zupi,Grande,Zucchin,Manfred,Torelli,Ferrari}
En consultant la matrice nous pouvons voir que le groupe 4 est constitué d'auteurs qui n'ont publié qu'avec Frances se sont peut-être ses "disciples"
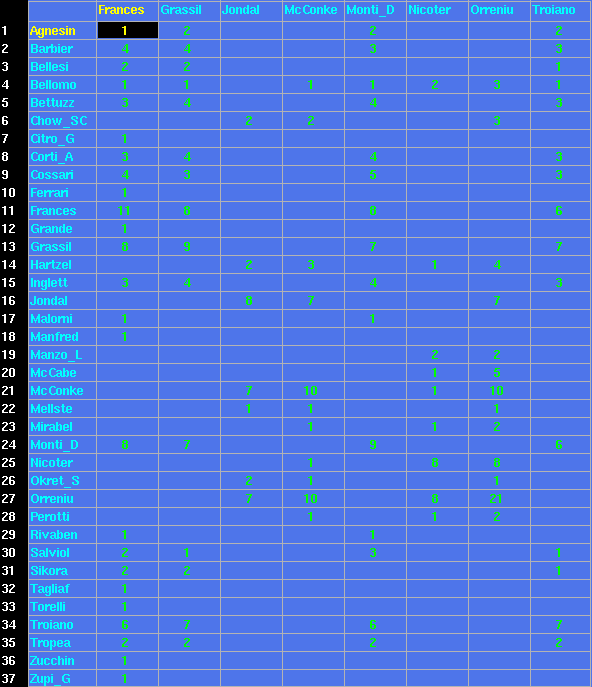
Nous remarquons que le groupe 2 en l'occurrence Bellomo semble faire le lien entre les groupes 1 dont les noms sont à consonance latine et le groupe 3 dont les noms ont une consonance anglo-saxonne. Pour vérifier cette hypothèse nous éliminons bellomo et nous reappliquons les algorithmes de recherche des réseaux indépendants de collaboration dans la matrice résultat. Nous remarquons alors qu'il y avait bien deux groupes distincts comme le montre la matrice diagonale par bloc suivante: